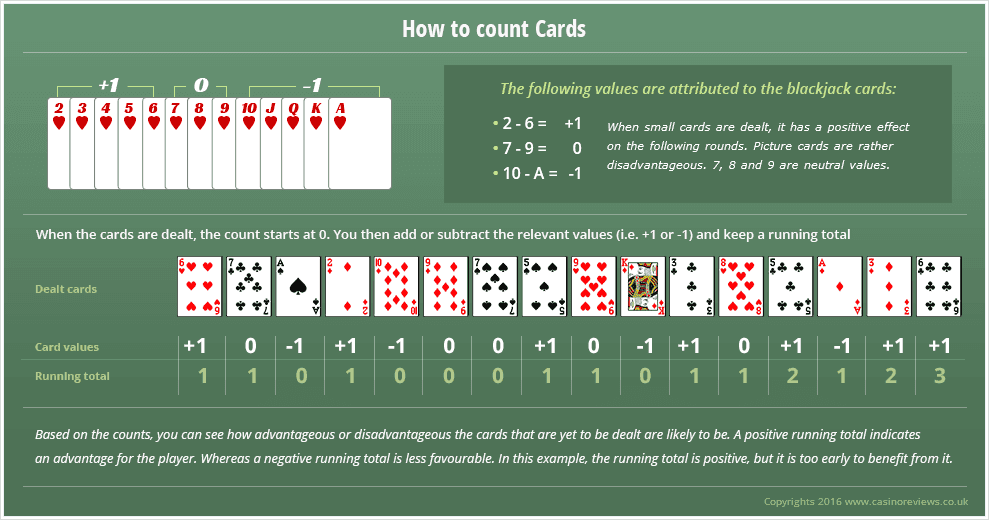
At what count/true count should you start betting? I'm very new to counting, I've been practicing with a deck of cards. I recently learned about the true count - is it more optimal to use than the running count? Feb 13, 2019 Yes No. True Count of Running Count 21 Half Decks 6 Say you have a running count of 21 and to get the true count you must divide the running count by the number of half decks. In this case let's say there are 6 half decks remaining.
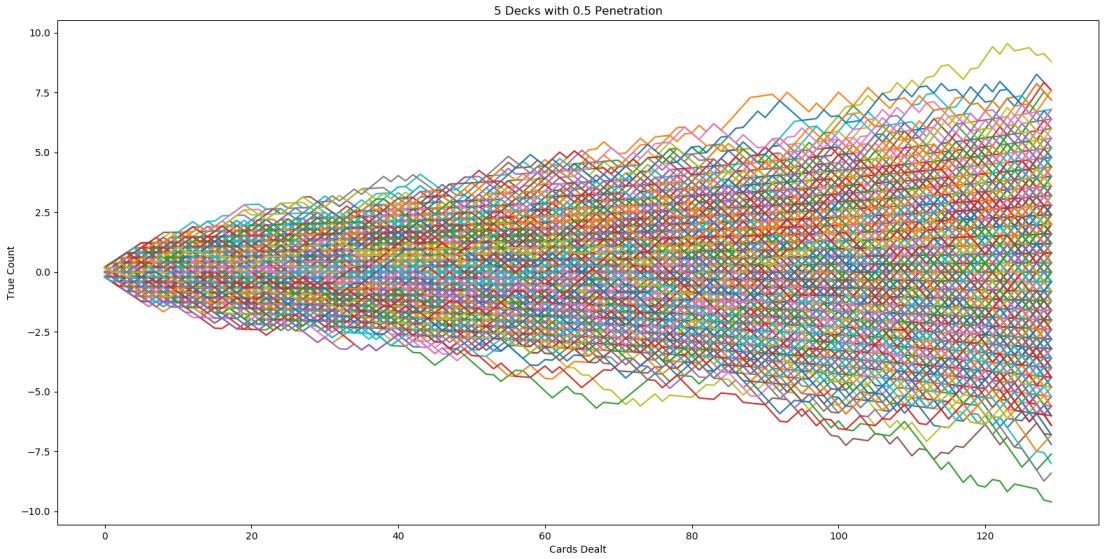
Blackjack True Count Chart
Six Deck Unbalanced Red 7 Running Count Conversion to Equivalent Hi-Lo Balanced True Count and Sensitivity of True Count to Errors in Estimating Decks Remaining
By Conrad Membrino(From Blackjack Forum Vol. XVII #4, Winter 1997)
© Blackjack Forum 1997
Running Count Blackjack
| rc.u = 23456p + (7p/2) - TAp |
Red-7 is almost equivalent to hi-lo count + counting all the sevens as (1/2) each.
rc.u = unbalanced running count = 23456+ (7p/2) - TAp
tc.b = balanced true count
n = number of decks
dp = decks played
dr = decks remaining
rc.u(tc.b) = unbalanced running count corresponding to a balance true count of tc.b
rc.hl = hi=lo running count = 23456p - TAp
rc.u = hi-lo + (7p)/2
if hi-lo has a true count of 't' then rc.hl = t*dr and
rc.u = rc.hl + ExpVal(7p)/2 = t*dr + 2*dp = (t+2-2)*dr + 2*dp = (t-2)*dr + 2*n
| rc.u = 2*n + (tc.b - 2) * dr |
Number of Decks = 6
Red-7 Running Counts Corresponding to Various True Counts for a Six Deck Game
| Six Deck Game | rc.unbal | |||||
| rc.unbal = 23456 + (7p/2) - TAp | decks played | |||||
| tc.bal | rc.unbal | 1 | 2 | 3 | 4 | 5 |
| 0 | 12 - 2*dr | 2 | 4 | 6 | 8 | 10 |
| 1 | 12 - dr | 7 | 8 | 9 | 10 | 11 |
| 2 | 12 | 12 | 12 | 12 | 12 | 12 |
| 3 | 12 + dr | 17 | 16 | 15 | 14 | 13 |
| 4 | 12 + 2*dr | 22 | 20 | 18 | 16 | 14 |
Sensitivity of True Count to Errors in Estimating Decks Remaining
Estimation of True Count Using the Red 7:
| rc.r7 = red 7 running count | n = number of decks |
| tc = true count | dr = decks remaining |
| rc.r7 = 2*n + (tc - 2) * dr |
Number of Decks = 8
Red-7 Running Counts Corresponding to Various
True Counts for an Eight Deck Game
| Eight Deck Game | rc.r7 | |||||
| rc.r7 = 23456 + (7p/2) - TAp | decks played | |||||
| tc | rc.r7 | 3 | 4 | 5 | 6 | 7 |
| 2 | 16 | 16 | 16 | 16 | 16 | 16 |
| 3 | 16 + dr | 21 | 20 | 19 | 18 | 17 |
| 4 | 16 + 2*dr | 26 | 24 | 22 | 20 | 18 |
Estimation of true count with the Red 7
in an Eight Deck Game:
- Estimate decks remaining
- Compare Red 7 running count with 16, 16 + dr, or 16 + 2*dr for true counts of 2, 3, or 4
- Use calculated true count with High-Low strategy indices.*
(*Ed. Note: Membrino is suggesting here that you may use this true count method not only to estimate your advantage, but also to alter your strategy with all Hi-Lo strategy indices. This is not the way I have developed the Red 7 in the new Blackbelt, but if you used a Starting Count of 0, then you could use this true count methology with any standard set of Hi-Lo count-per-deck indices. --Arnold Snyder)
Sensitivity of True Count to Errors
in Estimating Decks Remaining:
- The closer to the pivot point, the less sensitive the true count is to errors in estimating the decks remaining.
- At the pivot point, the true count is independent of the decks remaining
- Pivot Point of the Red 7: True Count = 2
- Pivot Point of Hi-Lo: True Count = 0
- At True Counts ≥ 2:
(a) Red 7 is closer to its pivot point (tc=2) than the Hi-Lo is to its pivot point (tc=0)
(b) Red 7 is less sensitive to errors in estimating decks remaining when calculating true count.
(c) Red 7 gives more accurate true counts than Hi-Lo.
Example:

| A = Actual | E = Estimated |
| dr:a = actual dr | dr:e = estimated dr |
| tc:a = actual tc | tc:e = estimated tc |
Eight Decks
| r7 = red 7 | hl = hi-lo |
| tc.r7 = 2 + (rc.r7 - 16)/dr | tc.hl = rc.hl/dr |
Eight Decks
dr:a = 4 and tc:a = 3
| Red 7 | Hi-Lo | |||||
| estimated | error | estimated | error | |||
| dr:e | rc.r7 | tc:e | (tc:e - tc:a) | rc.hl | tc:e | (tc:e - tc:a) |
| 6 | 20 | 2.7 | -0.3 | 12 | 2.0 | -1.0 |
| 5 | 2.8 | -0.2 | 2.4 | -0.6 | ||
| 4 | 3.0 | 0.0 | 3.0 | 0.0 | ||
| 3 | 3.3 | 0.3 | 4.0 | 1.0 | ||
| 2 | 4.0 | 1.0 | 6.0 | 3.0 |
♠
Return to Blackjack Forum Professional Gambling Library
Return to Blackjack Forum Online Home