Wizard Recommends
This article aims to take you through an explanation of the best odds and the best bets available on the roulette table. For further advice about increasing your chances of winning at roulette, you can always refer to our roulette betting systems guide. Jan 15, 2016 The winning odds on the roulette table for American roulette are low.So, you are better off in making a bet on European roulette. The basic formula for statistics can be applied to roulette and it is used to know the odds often.But, most of the computed odds for diverse bets in roulette. The table layout on the French version of roulette is different from the American style roulette table shown above. The main difference is in the position of the side bets (outside bets). The side bets on the French table are split in two and run along both sides of the table layout.
- €1500 Welcome Bonus
- €100 + 300 Free Spins
- 100% Welcome Bonus

On This Page
Introduction
The following table shows the house edge of most casino games. For games partially of skill perfect play is assumed. See below the table for a definition of the house edge.
Casino Game House Edge
| Game | Bet/Rules | House Edge | Standard Deviation |
|---|---|---|---|
| Baccarat | Banker | 1.06% | 0.93 |
| Player | 1.24% | 0.95 | |
| Tie | 14.36% | 2.64 | |
| Big Six | $1 | 11.11% | 0.99 |
| $2 | 16.67% | 1.34 | |
| $5 | 22.22% | 2.02 | |
| $10 | 18.52% | 2.88 | |
| $20 | 22.22% | 3.97 | |
| Joker/Logo | 24.07% | 5.35 | |
| Bonus Six | No insurance | 10.42% | 5.79 |
| With insurance | 23.83% | 6.51 | |
| Blackjacka | Liberal Vegas rules | 0.28% | 1.15 |
| Caribbean Stud Poker | 5.22% | 2.24 | |
| Casino War | Go to war on ties | 2.88% | 1.05 |
| Surrender on ties | 3.70% | 0.94 | |
| Bet on tie | 18.65% | 8.32 | |
| Catch a Wave | 0.50% | d | |
| Craps | Pass/Come | 1.41% | 1.00 |
| Don't pass/don't come | 1.36% | 0.99 | |
| Odds — 4 or 10 | 0.00% | 1.41 | |
| Odds — 5 or 9 | 0.00% | 1.22 | |
| Odds — 6 or 8 | 0.00% | 1.10 | |
| Field (2:1 on 12) | 5.56% | 1.08 | |
| Field (3:1 on 12) | 2.78% | 1.14 | |
| Any craps | 11.11% | 2.51 | |
| Big 6,8 | 9.09% | 1.00 | |
| Hard 4,10 | 11.11% | 2.51 | |
| Hard 6,8 | 9.09% | 2.87 | |
| Place 6,8 | 1.52% | 1.08 | |
| Place 5,9 | 4.00% | 1.18 | |
| Place 4,10 | 6.67% | 1.32 | |
| Place (to lose) 4,10 | 3.03% | 0.69 | |
| 2, 12, & all hard hops | 13.89% | 5.09 | |
| 3, 11, & all easy hops | 11.11% | 3.66 | |
| Any seven | 16.67% | 1.86 | |
| Double Down Stud | 2.67% | 2.97 | |
| Heads Up Hold 'Em | Blind pay table #1 (500-50-10-8-5) | 2.36% | 4.56 |
| Keno | 25%-29% | 1.30-46.04 | |
| Let it Ride | 3.51% | 5.17 | |
| Pai Gowc | 1.50% | 0.75 | |
| Pai Gow Pokerc | 1.46% | 0.75 | |
| Pick ’em Poker | 0% - 10% | 3.87 | |
| Red Dog | Six decks | 2.80% | 1.60 |
| Roulette | Single Zero | 2.70% | e |
| Double Zero | 5.26% | e | |
| Sic-Bo | 2.78%-33.33% | e | |
| Slot Machines | 2%-15%f | 8.74g | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | d |
| Dealer stands on soft 17 | 0.40% | d | |
| Super Fun 21 | 0.94% | d | |
| Three Card Poker | Pairplus | 7.28% | 2.85 |
| Ante & play | 3.37% | 1.64 | |
| Video Poker | Jacks or Better (Full Pay) | 0.46% | 4.42 |
| Wild Hold ’em Fold ’em | 6.86% | d |
Notes
| a | Liberal Vegas Strip rules: Dealer stands on soft 17, player may double on any two cards, player may double after splitting, resplit aces, late surrender. |
| b | Las Vegas single deck rules are dealer hits on soft 17, player may double on any two cards, player may not double after splitting, one card to split aces, no surrender. |
| c | Assuming player plays the house way, playing one on one against dealer, and half of bets made are as banker. |
| d | Yet to be determined. |
| e | Standard deviation depends on bet made. |
| f | Slot machine range is based on available returns from a major manufacturer |
| g | Slot machine standard deviation based on just one machine. While this can vary, the standard deviation on slot machines are very high. |
House Edge
The house edge is defined as the ratio of the average loss to the initial bet. The house edge is not the ratio of money lost to total money wagered. In some games the beginning wager is not necessarily the ending wager. For example in blackjack, let it ride, and Caribbean stud poker, the player may increase their bet when the odds favor doing so. In these cases the additional money wagered is not figured into the denominator for the purpose of determining the house edge, thus increasing the measure of risk.
Betting Odds Comparison
The reason that the house edge is relative to the original wager, not the average wager, is that it makes it easier for the player to estimate how much they will lose. For example if a player knows the house edge in blackjack is 0.6% he can assume that for every $10 wager original wager he makes he will lose 6 cents on the average. Most players are not going to know how much their average wager will be in games like blackjack relative to the original wager, thus any statistic based on the average wager would be difficult to apply to real life questions.
The conventional definition can be helpful for players determine how much it will cost them to play, given the information they already know. However the statistic is very biased as a measure of risk. In Caribbean stud poker, for example, the house edge is 5.22%, which is close to that of double zero roulette at 5.26%. However the ratio of average money lost to average money wagered in Caribbean stud is only 2.56%. The player only looking at the house edge may be indifferent between roulette and Caribbean stud poker, based only the house edge. If one wants to compare one game against another I believe it is better to look at the ratio of money lost to money wagered, which would show Caribbean stud poker to be a much better gamble than roulette.
Many other sources do not count ties in the house edge calculation, especially for the Don’t Pass bet in craps and the banker and player bets in baccarat. The rationale is that if a bet isn’t resolved then it should be ignored. I personally opt to include ties although I respect the other definition.
Element of Risk
For purposes of comparing one game to another I would like to propose a different measurement of risk, which I call the 'element of risk.' This measurement is defined as the average loss divided by total money bet. For bets in which the initial bet is always the final bet there would be no difference between this statistic and the house edge. Bets in which there is a difference are listed below.
Element of Risk
| Game | Bet | House Edge | Element of Risk |
|---|---|---|---|
| Blackjack | Atlantic City rules | 0.43% | 0.38% |
| Bonus 6 | No insurance | 10.42% | 5.41% |
| Bonus 6 | With insurance | 23.83% | 6.42% |
| Caribbean Stud Poker | 5.22% | 2.56% | |
| Casino War | Go to war on ties | 2.88% | 2.68% |
| Heads Up Hold 'Em | Pay Table #1 (500-50-10-8-5) | 2.36% | 0.64% |
| Double Down Stud | 2.67% | 2.13% | |
| Let it Ride | 3.51% | 2.85% | |
| Spanish 21 | Dealer hits soft 17 | 0.76% | 0.65% |
| Spanish 21 | Dealer stands on soft 17 | 0.40% | 0.30% |
| Three Card Poker | Ante & play | 3.37% | 2.01% |
| Wild Hold ’em Fold ’em | 6.86% | 3.23% |
Standard Deviation
The standard deviation is a measure of how volatile your bankroll will be playing a given game. This statistic is commonly used to calculate the probability that the end result of a session of a defined number of bets will be within certain bounds.
The standard deviation of the final result over n bets is the product of the standard deviation for one bet (see table) and the square root of the number of initial bets made in the session. This assumes that all bets made are of equal size. The probability that the session outcome will be within one standard deviation is 68.26%. The probability that the session outcome will be within two standard deviations is 95.46%. The probability that the session outcome will be within three standard deviations is 99.74%. The following table shows the probability that a session outcome will come within various numbers of standard deviations.
I realize that this explanation may not make much sense to someone who is not well versed in the basics of statistics. If this is the case I would recommend enriching yourself with a good introductory statistics book.
Standard Deviation
What Are The Best Odds On A Roulette Table Game
| Number | Probability |
|---|---|
| 0.25 | 0.1974 |
| 0.50 | 0.3830 |
| 0.75 | 0.5468 |
| 1.00 | 0.6826 |
| 1.25 | 0.7888 |
| 1.50 | 0.8664 |
| 1.75 | 0.9198 |
| 2.00 | 0.9546 |
| 2.25 | 0.9756 |
| 2.50 | 0.9876 |
| 2.75 | 0.9940 |
| 3.00 | 0.9974 |
| 3.25 | 0.9988 |
| 3.50 | 0.9996 |
| 3.75 | 0.9998 |
Hold
Although I do not mention hold percentages on my site the term is worth defining because it comes up a lot. The hold percentage is the ratio of chips the casino keeps to the total chips sold. This is generally measured over an entire shift. For example if blackjack table x takes in $1000 in the drop box and of the $1000 in chips sold the table keeps $300 of them (players walked away with the other $700) then the game's hold is 30%. If every player loses their entire purchase of chips then the hold will be 100%. It is possible for the hold to exceed 100% if players carry to the table chips purchased at another table. A mathematician alone can not determine the hold because it depends on how long the player will sit at the table and the same money circulates back and forth. There is a lot of confusion between the house edge and hold, especially among casino personnel.
Hands per Hour, House Edge for Comp Purposes
The following table shows the average hands per hour and the house edge for comp purposes various games. The house edge figures are higher than those above, because the above figures assume optimal strategy, and those below reflect player errors and average type of bet made. This table was given to me anonymously by an executive with a major Strip casino and is used for rating players.
Hands per Hour and Average House Edge
| Games | Hands/Hour | House Edge |
|---|---|---|
| Baccarat | 72 | 1.2% |
| Blackjack | 70 | 0.75% |
| Big Six | 10 | 15.53% |
| Craps | 48 | 1.58% |
| Car. Stud | 50 | 1.46% |
| Let It Ride | 52 | 2.4% |
| Mini-Baccarat | 72 | 1.2% |
| Midi-Baccarat | 72 | 1.2% |
| Pai Gow | 30 | 1.65% |
| Pai Pow Poker | 34 | 1.96% |
| Roulette | 38 | 5.26% |
| Single 0 Roulette | 35 | 2.59% |
| Casino War | 65 | 2.87% |
| Spanish 21 | 75 | 2.2% |
| Sic Bo | 45 | 8% |
| 3 Way Action | 70 | 2.2% |
Translation
A Spanish translation of this page is available at www.eldropbox.com.
Written by: Michael Shackleford
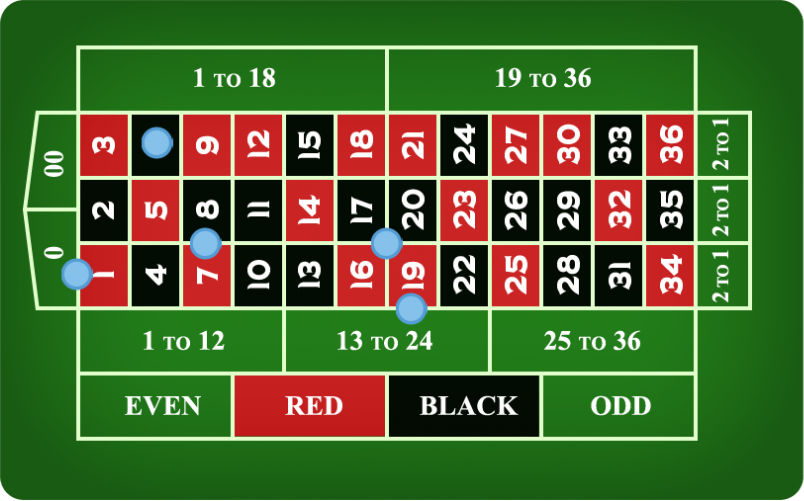
Roulette offers a bewildering number of betting options, but the bets are actually straightforward enough. In order to make sure you get the correct payout, you’ll want to make sure that you put your chips in exactly the right place on the table. Missing a payout because your chip isn’t in the right spot is a drag.
Roulette payouts work like this. The odds are stated in the form of x to 1, which means you’ll win x dollars for every dollar you’ve bet. For example, the single number bet offers a payout of 35 to 1. If you win, you’ll get your dollar back plus the $35 for the win.
Payouts on the Outside Bets
On the edge of the table are a series of bets which are “outside” the 38 numbers on the table. Each of these bets refers to a specific set of numbers or colors. If the ball lands on 0 or 00, you’ll lose on any of the outside bets.
The outside bets include:
Red or Black – This bet pays out even odds (1 to 1) if the ball lands on the color you chose.
Odd or Even – This bet pays out even odds (1 to 1) if the ball lands on odd or even, depending on which you chose.
Low or High – This bet pays out even money (1 to 1) if the ball lands on 1-18 if you bet low, or if the ball lands on 19-36 if you bet high.
Columns – The numbers on the layout are organized into three columns of twelve numbers each. A “columns” bet wins if the ball lands on one of the numbers in the column you chose. This bet pays out 2 to 1 when you win.
Dozens – There are 36 numbers on the table, so you can bet on the first dozen (1-12), the second dozen (13-24), or the third dozen (25-36). This bet also pays out 2 to 1.
Payouts on the Inside Bets
You can also bet on specific numbers and sets of numbers on the inside of the layout. These bets win less often, but they pay out more when you do win. The house edge on the inside bets is the same as the house edge on the outside bets.
The inside bets include:
Straight-up – This is a bet on a single number. It pays off at 35 to 1.
Split bet – This is a bet on any two adjacent numbers. You place the chip on the line between the two numbers in order to make this wager. This bet pays out at 17 to 1.
Street bet – This bet covers three numbers. You place your bet on the line outside of the three numbers in the row where you want to win. This bet pays out at 11 to 1.
Corner bet – Some people call this a square bet or a quarter bet. It’s a bet on a corner that makes a square, and it’s a bet on four numbers. A win on this type of bet pays out at 8 to 1.
Five-number bet – You can only make one five-number bet, and it’s the only inside bet that offers different odds from all the others. The problem is that it has a higher house edge, making it the worst bet on the table. This bet is on the numbers 0, 00, 1, 2, and 3, and you place the chip on the outside corner line between the 1 and the 0. This bet pays out 6 to 1, but only masochists place this bet.
Six-number bet – Some people call this a line bet. It covers two adjoining rows of numbers. It pays out at 5 to 1.
How Roulette Payouts Give the Casino an Edge
These payouts all have one thing in common—they pay out less than the true odds of hitting a win. That’s why the casino enjoys a house edge of 5.26% on roulette. Your odds of winning are always less than the payout amounts.
For example, the odds of winning a straight-up bet are 37 to 1. There are 37 numbers on the wheel that lose, and 1 bet on the wheel that will win. But the bet only pays out 35 to 1, not 37 to 1, so the house wins more often than it loses.
A split bet offers you odds of winning of 18 to 1, but it pays off at 17 to 1.
I could list all of them, but you get the idea by now. The casino has an unassailable mathematical advantage on every bet. No betting system or strategy can overcome this advantage.
Of course, in the short run, anything can (and often will) happen. This is called “standard deviation”, and it explains why some people walk away from the roulette table as winners. The mathematically true results only come around the closer you get to an infinite number of spins.
So the best way to approach roulette is as a lark. It’s a fun game. You can relax and socialize while you play. But don’t expect to win, because the odds are against you. And if you do win, walk away and smile, because you beat the odds.